Background
In my personal projects, I often work with various sensors which require digital data verification. One such sensor required the use of a Cyclic Redundancy Check (CRC) to verify that the information that the micro-controller read from the sensor was being received correctly. A CRC is a method for calculating a checksum from an array of data. The software examples that I was able to find to develop my understanding of implementing a CRC were poorly documented. Moreover, these examples were often so optimized that the underlying behavior was not immediately recognizable. Many examples simply used a lookup table—which provided no satisfaction for my “what-makes-it-tick?” personality.
How does a CRC verify data integrity?
Suppose a digital sensor transmits a data frame of 5 data bytes of information with another 1 byte checksum. The recipient can then perform the CRC on the 5 data bytes it receives and compares that result with the received checksum from the sensor. If the checksums are different, then the recipient recognizes that as bad data and has to discard it until the next 6-byte frame is received for verification. If the checksums are identical, then the received data is interpreted as correct.
The approach that I will use as an example is the most low-level software technique that can be implemented. This method is essentially a modified shift register, depicted in Figure 1, which steps through each bit, one by one. Ultimately it is much more efficient to use a lookup table or a byte-by-byte approach, but those examples are plentiful.
The CRC contains XOR gates which allow it to iteratively compute the checksum. There is no output as one might think of in terms of a FIFO or LIFO system, but rather the register content is the output. When all of the input data bits are processed by the register, then the register content—formally known as the result or remainder—is the final checksum.
Figure 1 shows a 9-bit CRC with an 8-bit result. The larger the dataset to be processed, the larger the recommended CRC width should be. There exist 32- and 64-bit CRCs.
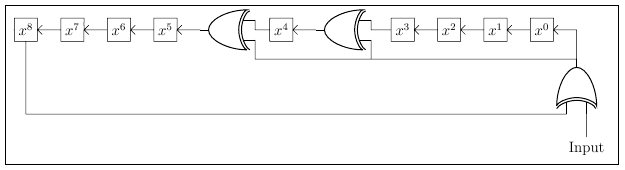
A CRC register starts out with an initial value of all zeros or all ones as declared by the CRC specification that is being used. As each input bit fills the register, the shifting will produce a carry bit in the most significant bit of the register (x8 Figure Figure 1). If the carry bit XORed with the Input Bit results in a 0, then simply shift the register. If the carry bit XORed with the Input Bit is a 1, then both shift and also XOR the register contents with the polynomial.
Characterizing a CRC
Definitions
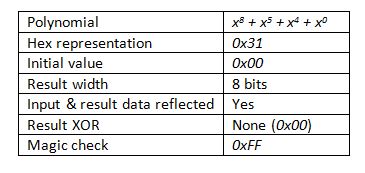
Polynomial A polynomial is a representation of where the XOR gates are located in the shift register. The xn in the polynomial, x8 + x5 + x4 + x0, of Figure 1 represents the location of an XOR gate. The hexadecimal representation of this polynomial is 0x31 (0011 00012), matching the bitfield of the terms in the polynomial. Note that the x8 term is not included as it would be the highest order term, and the highest order term is always implicit. If it were not implicit, then including it would make the result a 9-bit value.
Initial Value The register needs an initialization value at the start of the calculation. Most of the time the initialization value is zero, but some CRC specifications call for all ones in the register.
CRC Result Width An [n]-bit CRC has an [n-1]-bit result. The polynomial x8 + x5 + x4 + x0, for example, would have an 8-bit result.
Input Data Reflected Some CRC specifications specify a reflected (i.e. reversed or mirrored) bitfield in each byte. That is, if the input data is not reflected, then the bits are fed into the CRC register from the MSBit first. If the input data is reflected, then the bits are processed from the LSBit first. Note that this reflection does not dictate the byte order—which is always MSByte first.
Result Data Reflected For CRCs which require reflected input data, then reflecting the result is also required. If an 8-bit unreflected result is 0x31 (0011 00012), then the reflected result would be 0x8C (1000 11002).
XOR Result Depending on the CRC specification, a CRC result may need to be XORed with all zeros or all ones before it is returned as the official checksum.
Magic Check The “Magic Check” is a value that is used to verify the implementation of a checksum. It is often used when there are no known tables, examples, or other validation techniques to verify during unit testing. If the magic check is XORed with CRC result of the original data appended with its corresponding CRC, then the result is 0xFF.
Magic Check example: Suppose a checksum, 0x59, is generated from the input [0x00 , 0x00 , 0x00] for a polynomial which has a magic check value of 0xC4. To perform this validation technique, the CRC would be appended as the new least-significant byte, [0x59 , 0x00 , 0x00 , 0x00], and then a CRC is generated from that data. The CRC result of this (4-byte) data is then 0x3B, which XORed with the magic check for this polynomial (0xC4) then becomes 0xFF.
Walk through example
Before implementing a CRC in software, the following specifications need to be known.
1. The polynomial (this determines the hex representation and result width)
2. Initial value
3. Is the input and result data reflected?
4. Is the result XORed with a specified value before being returned as the checksum?
Suppose a checksum for the following CRC specification needs to be generated for an input byte of 0x12 (0001 00102).
Table 1: Specifications of a CRC-8
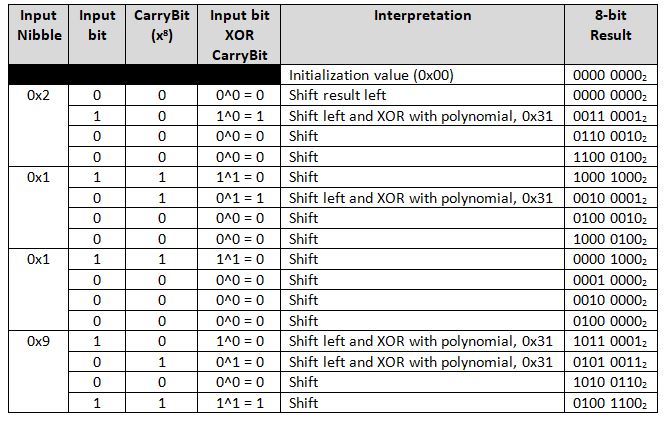
This is a bitwise walk through of calculating the CRC-8 mentioned above, for a value of [0x91, 0x12] (1001 00012, 0001 00102). As this polynomial uses a reflected input and result, then then input is fed from the LSBit of the MSByte first, ending with the MSBit of the LSByte.
Table 2: Walk through of CRC-8 Checksum Calculation
The result is then 0x4C, which still needs to be reflected as per the specifications, thereby producing a checksum of: 0x32.
Performing a magic check against [0x32, 0x91, 0x12] produces a value of 0x00. XORing this result, 0x00, with the magic check of 0xFF, produces 0xFF, thereby verifying that the algorithm is correct.